Oct 4: Abstract Classes. Review of Algorithm Analysis.


Code discussed in lecture

Access Control

We have talked about public and private access. Those are the kinds of access that we will usually use. However, you should know that there are four access levels:

  1. public access,
  2. private access,
  3. protected access, and
  4. package access (which is the default when no other access is specified).
We have seen that public access means that any method of any class can access the variable or method. Private access is limited to the given class and its inner classes.

Protected access is new for us. With protected access, the variable or method should be accessible to only the class and any subclass that extends the class (or extends a class that extends the class, etc.). Protected access seems to be a good compromise between public and private, and it is certainly an improvement on public.

There is a problem with protected access, however. Because anyone can extend a class, there is no real control over who can access protected instance variables. Again, there is no abstraction barrier between the superclass and its subclasses. A better way to restrict access is to make all instance variables (except constants) private and then to make the methods that can access those instance variables protected. That should prevent classes other than subclasses from accessing the instance variables, while still keeping encapsulation.

The default access, package access, is what you get if you don't put anything before the instance variable or method. In other words, it's what you'd get for the instance variable x in the following class:

public class Bozo { int x; // package access ... }

I consider it a design flaw of the language that there is no package visibility level specifier, as there is for public, private, and protected. It is too easy to forget to declare an instance variable (or method) private. I would have preferred that leaving off the visibility level specifier would be a syntax error. That way the programmer would always have to make an explicit choice.

Package access makes the variable or method visible to everything in the same package. As we mentioned when we talked about import statements, package is a way of grouping methods together that are intended to work together as a group, like java.util or java.awt. To put a file into a package, you start the file with a package statement:

package packageName;

If there is not a package statement, then all classes in the file go into the default package.

You seldom want package access. Anyone can add a class to a package, so you have very little control of who has access to things that have package access. It sometimes makes sense to give package access for methods that you want as utility routines within a package, but it seldom makes sense to have package access for instance variables.

You may have noticed that when I described what protected means, I said it "should" only be available to the class and its descendents (subclasses or subclasses of those subclasses, etc.). That is what protected means in C++. Unfortunately, that is not what it means in Java. As we have described it, public is the least restrictive, private the most, and protected and package are both somewhere in between, but you can't say that one is more restrictive than the other. They control access in very different ways.

The designers of Java decided that not having a linear heirarchy of protection levels was a bad idea. Therefore they somewhat arbitrarily decided that protected access should include package access, so that package access is more restrictive than protected. So in Java protected really means visible in descendents and to classes in the same package. If you are using the default package, that means it is not much different than public! However, I will still declare things protected to indicate who should have access.

Abstract Classes and a Hierarchy of Graphical Objects

In a previous lecture we used an interface to allow ourselves to define a variable declared to be a reference to a GeomShape. In fact, GeomShape was an interface, and the way we implemented the program, the variable was actually a reference to either a Circle or a Rectangle object. We can accomplish the same thing via inheritance and avoid duplicating code in the process.

Consider geometric shapes: circles, rectangles, segments, squares, diamonds, etc. What do they have in common? We might want all of them to have a color, to know how to draw themselves, to know how to move themselves, and to know how to compute their area. The class GeomShape.java defines a class with these properties. Note that all shapes will have a color, and so myColor is an instance variable that is initialized in a constructor. There are methods to set and get the color. The draw method doesn't know how to draw the object, but we will look later at how it can allow the shape to be drawn in the correct color without permanently changing the color of the Graphics object.

The methods areaOf and move depend on specific information about the shape. Therefore they are given as abstract methods. The header ends in a semicolon and the word abstract is included in the header. The entire class is also declared as abstract. No object of an abstract class can ever be created. Hence, no GeomShape object can be created. Abstract classes exist only to serve as superclasses for other classes.

If a class declares one or more abstract methods, then the class itself must be declared abstract. However, you can still declare a class to be abstract even if it declares no abstract methods. As before, declaring a class to be abstract means that no object of the class can be created (even if the class contains no abstract methods).

A second abstract class, PointRelativeShape.java, is a subclass of GeomShape. This class is for shapes that have some "center" or reference point, where the shape is defined relative to that reference point.

PointRelativeShape takes care of defining the instance variables myX and myY, providing methods to return these values, and providing the move method. It extends GeomShape. Even though it declares no methods as abstract, it fails to implement areaOf, so it must be abstract as well.

Finally, Circle.java and Rect.java inherit from PointRelativeShape. Note the use of super in the constructors. The draw methods use super.draw to deal with the color, and getX and getY to figure out where the object is. They do not have to supply a move method, because they inherit it.

We can also have classes that inherit directly from GeomShape. Segment.java does so, and it implements everything itself.

Here's a picture of our class hierarchy:

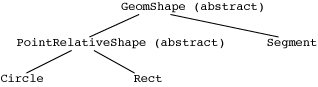
Now, let's look at the driver GeomShapeDriver.java, which demonstrates all of these classes, showing that everything works. Again, we see polymorphism in action. The variable shape is declared as a reference to GeomShape, but in reality it will refer to a Circle, Rect, or Segment object. The calls at the bottom of the loop body show dynamic binding in action. The first time through the loop, we call methods in the Circle class; the second time through, we call methods in the Rect class; and the third time through, we call methods in the Segment class.

How to leave the current color alone when drawing an object

So far when we went to draw a shape we set the color of the Graphics object and drew our shape. This means that the next time we draw something it will be in the color of the last shape drawn. If we are doing something like using drawString to print information that the text will be in that color. Suppose we wanted the text to remain whatever the original foreground color was?

How can we solve this problem? The Graphics class has a getter method that returns the current color for drawing: getColor. Thus, we can solve the problem by making the draw methods in the subclasses save the current color by calling getColor, changing the Graphics object's color to the color of the object being drawn, drawing the object, and finally restoring the saved color. For the Circle class, we'd rewrite draw as follows:

public void draw(Graphics page) { // Save the current color. Color savedColor = page.getColor(); // Set the color. super.draw(page); // Draw the circle. page.drawOval(getX() - myRadius, getY() - myRadius, 2*myRadius, 2*myRadius); // Restore the color we had on the way in. page.setColor(savedColor); }

Unfortunately, that's a lot of work that we'd have to repeat for each instantiable subclass of GeomShape. There's a better way to accomplish this goal, with less code. We move all of the code except the actual drawing of the shape up to the GeomShape class in GeomShape.java to add the following abstract method:

protected abstract void drawShape(Graphics page);

Note that this is an example of the template pattern. The draw method does all of the color saving, changing, and restoring and leaves the detail of how to draw the shape to an abstract method.

Each instantiable class will have to define the drawShape method, and it would consist of the code that is specialized to that shape. For example, here's the drawShape method in the Rect class, within Rect.java:

protected void drawShape(Graphics page) { page.drawRect(getX(), getY(), myWidth, myHeight); } You can see also how we wrote the drawShape methods in Circle.java and Segment.java.

Now we can understand the draw method in GeomShape. It saves the current color, sets the current color to the shape's actual color, does the drawing specialized to the shape, and finally restores the original color:

public void draw(Graphics page) { // Save the current color. Color savedColor = page.getColor(); // Set the color. page.setColor(myColor); // Draw the shape in the shape's color. drawShape(page); // Restore the color we had on the way in. page.setColor(savedColor); }

Once again, dynamic binding helps us. When the draw method calls drawShape, which class has its drawShape method called? As usual, it's the class of the object that draw was called on.

Why did I make drawShape protected? I intend drawShape to be called only by the draw method in GeomShape. By making it protected, it cannot be called by methods outside of GeomShape or its subclasses. (Well, except for the detail that any other class in the same package can call it, also!)

Because drawShape is protected in GeomShape, I had to make drawShape protected in the subclasses Circle, Rect, and Segment. That's because when we declare a method as abstract in a superclass, the method has to have at least the same degree of "visibility" in the subclasses. Why? When we say that a superclass allows a method to be called, that method has to be callable in all subclasses. So the method must be at least as visible in the subclasses as it is in the superclass.

Adapter Classes

When we created listeners, we had to implement an interface. For the MouseListener interface, there were five methods that had to be implemented, and we usually used only one or two. We had to create empty-bodied implementations for the others. Having to do so was a minor irritant.

This situation comes up often enough that Java has provided an alternate approach. For each Listener interface, there is a corresponding Adapter class that supplies empty-body implementations for each of the methods in the interface. We then can extend these classes, overriding just the methods that we want to actually do something. We no longer have to supply the empty-body implementations, because the Adapter class has already done that, and we inherit them.

For example, consider DragAMac3.java. It has two inner classes that implement the MouseListener and the MouseMotionListener interfaces. But instead of saying that we will implement these interfaces, we instead extend the MouseAdapter and MouseMotionAdapter classes. The empty-body implementations that we had before are now gone.

Note that if we use the applet itself as the listener (using this as the parameter to the appropriate addListener method calls), we cannot use this approach. That is because in creating the class DragAMac, we have already extended Applet, and Java does not allow multiple inheritance. In other words, Java does not allow a class to extend more than one other class. DragAMac has to extend Applet, and we can either implement the two interfaces directly or extend the Adapter classes in inner classes as we have done here. In fact, we had to use two different inner classes, since a single inner class cannot extend both Adapter classes.

We saw one other interface that we use to handle events: the ActionListener interface. Unlike MouseListener and MouseMotionListener, ActionListener has no corresponding adapter class. There's a pretty good reason for that. What do you think it is?

Inheritance vs. interfaces

The above point is worth repeating.
In Java, a subclass can extend just one superclass.
(Extending more than one superclass would be multiple inheritance.) For example, the following class declaration would not be legal: class Bozo extends Clown, TVStar { ... } On the other hand, a class is allowed to implement any number of interfaces. Thus, the following class declaration would be legal: class Bozo implements Clown, TVStar { ... }

Why doesn't Java allow multiple inheritance? Because it can cause problems that are difficult to resolve. What if more than one superclass defines the same instance variable that is visible to the subclass (i.e., either public or protected)? What if more than one superclass defines a method with the same name and signature? What if you have a "diamond" shaped inheritance structure, where A is the superclass, B and C both inherit from A, and D inherits from both B and C. D should have access to all instance variables that B and C have. But each has a copy of A's instance variables! Should D have two copies of each?

C++ allows multiple inheritance, and it pays the price in its complexity. The designers of Java decided to keep things simple, and so Java does not provide for multiple inheritance. Interfaces provide a way to get most of the benefits of multiple inheritance without most of the problems. The downside of interfaces, of course, is that they don't allow you to define instance variables in them, nor do they allow you to provide method bodies that are inherited.

Analysis of Algorithms

Almost everyone in the class has see big-O notation and big-Theta notation. Therefore I did a brief overview of them in class today. However, I will include some notes from CS 5 below (with some additions to talk about big-Omega notation) for those who have not seen this material. The book does a good job of explaining them in Chapter 4, and you should definitely read it!

I ended class with a problem for people to work on before next class. Suppose you have a program that runs the insertion sort algorithm, whose worst and average case run times are Θ(n2), where n is the number of items to sort. Someone has given you a list of 10,000 randomly ordered things to sort. Your program takes 0.1 seconds. Then you are sent a list of 1,000,000 randomly ordered things to sort. How long do you expect your program to take? Should you wait? Get coffee? Go to dinner? Go to bed? How can you decide?

Order of growth

Binary searching through n elements requires time c7 lg n + c8 vs. linear search's running time of c5 n + c6. Where linear search has a linear term, binary search has a logarithmic term. We also saw that lg n grows much more slowly than n; for example, when n = 1,000,000,000 (a billion), lg n is approximately 30.

If we consider only the leading terms and ignore the coefficients for running times, we can say that in the worst case, linear search's running time "grows like" n and binary search's running time "grows like" lg n. This notion of "grows like" is the essence of the running time. Computer scientists use it so frequently that we have a special notation for it: "big-Oh" notation, which we write as "O-notation."

For example, the running time of linear search is always at most some linear function of the input size n. Ignoring the coefficients and low-order terms, we write that the running time of linear search is O(n). You can read the O-notation as "order." In other words, O(n) is read as "order n." You'll also hear it spoken as "big-Oh of n" or even just "Oh of n."

Similarly, the running time of binary search is always at most some logarithmic function of the input size n. Again ignoring the coefficients and low-order terms, we write that the running time of binary search is O(lg n), which we would say as "order log n," "big-Oh of log n," or "Oh of log n."

In fact, within our O-notation, if the base of a logarithm is a constant (like 2), then it doesn't really matter. That's because of the formula

loga n = (logb n) / (logb a)
for all positive real numbers a, b, and c. In other words, if we compare loga n and logb n, they differ by a factor of logb a, and this factor is a constant if a and b are constants. Therefore, even though we use the "lg" notation within O-notation, it's irrelevant that we're really using base-2 logarithms.

O-notation is used for what we call "asymptotic upper bounds." By "asymptotic" we mean "as the argument (n) gets large." By "upper bound" we mean that O-notation gives us a bound from above on how high the rate of growth is.

Here's the technical definition of O-notation, which will underscore both the "asymptotic" and "upper-bound" notions:

A running time is O(n) if there exist positive constants n0 and c such that for all problem sizes n ≥ n0, the running time for a problem of size n is at most cn.

Here's a helpful picture:

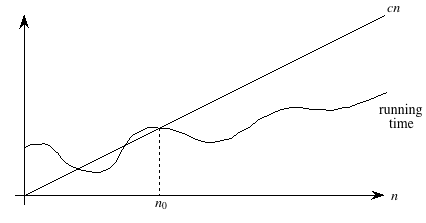
The "asymptotic" part comes from our requirement that we care only about what happens at or to the right of n0, i.e., when n is large. The "upper bound" part comes from the running time being at most cn. The running time can be less than cn, and it can even be a lot less. What we require is that there exists some constant c such that for sufficiently large n, the running time is bounded from above by cn.

For an arbitrary function f(n), which is not necessarily linear, we extend our technical definition:

A running time is O(f(n)) if there exist positive constants n0 and c such that for all problem sizes n ≥ n0, the running time for a problem of size n is at most c f(n).
A picture:

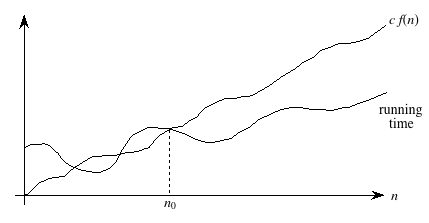
Now we require that there exist some constant c such that for sufficiently large n, the running time is bounded from above by c f(n).

Actually, O-notation applies to functions, not just to running times. But since our running times will be expressed as functions of the input size n, we can express running times using O-notation.

In general, we want as slow a rate of growth as possible, since if the running time grows slowly, that means that the algorithm is relatively fast for larger problem sizes.

We usually focus on the worst case running time, for several reasons:

You might think that it would make sense to focus on the "average case" rather than the worst case, which is exceptional. And sometimes we do focus on the average case. But often it makes little sense. First, you have to determine just what is the average case for the problem at hand. Suppose we're searching. In some situations, you find what you're looking for early. For example, a video database will put the titles most often viewed where a search will find them quickly. In some situations, you find what you're looking for on average halfway through all the data…for example, a linear search with all search values equally likely. In some situations, you usually don't find what you're looking for…like at Radio Shack.

It is also often true that the average case is about as bad as the worst case. Because the worst case is usually easier to identify than the average case, we focus on the worst case.

Computer scientists use notations analogous to O-notation for "asymptotic lower bounds" (i.e., the running time grows at least this fast) and "asymptotically tight bounds" (i.e., the running time is within a constant factor of some function). We use Ω-notation (that's the Greek leter "omega") to say that the function grows "at least this fast". It is almost the same as Big-O notation, except that is has an "at least" instead of an "at most":

A running time is Ω(n) if there exist positive constants n0 and c such that for all problem sizes n ≥ n0, the running time for a problem of size n is at least cn.
We use Θ-notation (that's the Greek letter "theta") for asymptotically tight bounds:
A running time is Θ(f(n)) if there exist positive constants n0, c1, and c2 such that for all problem sizes n ≥ n0, the running time for a problem of size n is at least c1 f(n) and at most c2 f(n).

Pictorially,

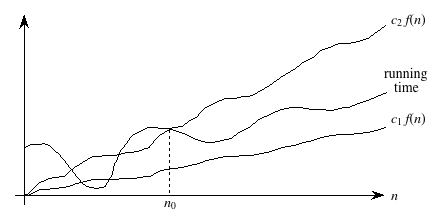
In other words, with Θ-notation, for sufficiently large problem sizes, we have nailed the running time to within a constant factor. As with O-notation, we can ignore low-order terms and constant coefficients in Θ-notation.

Note that Θ-notation subsumes O-notation in that

If a running time is Θ(f(n)), then it is also O(f(n)).
The converse (O(f(n)) implies Θ(f(n))) does not necessarily hold.

The general term that we use for either O-notation or Θ-notation is asymptotic notation.

Recap

Both asymptotic notations—O-notation and Θ-notation—provide ways to characterize the rate of growth of a function f(n). For our purposes, the function f(n) describes the running time of an algorithm, but it really could be any old function. Asymptotic notation describes what happens as n gets large; we don't care about small values of n. We use O-notation to bound the rate of growth from above to within a constant factor, and we use Θ-notation to bound the rate of growth to within constant factors from both above and below.

We need to understand when we can apply each asymptotic notation. For example, in the worst case, linear search runs in time proportional to the input size n; we can say that linear search's worst-case running time is Θ(n). It would also be correct, but less precise, to say that linear search's worst-case running time is O(n). Because in the best case, linear search finds what it's looking for in the first array position it checks, we cannot say that linear search's running time is Θ(n) in all cases. But we can say that linear search's running time is O(n) in all cases, since it never takes longer than some constant times the input size n.

Working with asymptotic notation

Although the definitions of O-notation and Θ-notation may seem a bit daunting, these notations actually make our lives easier in practice. There are two ways in which they simplify our lives.

I won't go through the math that follows in class. You may read it, in the context of the formal definitions of O-notation and Θ-notation, if you wish. For now, the main thing is to get comfortable with the ways that asymptotic notation makes working with a function's rate of growth easier.

Constant factors don't matter

Constant multiplicative factors are "absorbed" by the multiplicative constants in O-notation (c) and Θ-notation (c1 and c2). For example, the function 1000n2 is Θ(n2), since we can choose both c1 and c2 to be 1000.

Although we may care about constant multiplicative factors in practice, we focus on the rate of growth when we analyze algorithms, and the constant factors don't matter. Asymptotic notation is a great way to suppress constant factors.

Low-order terms don't matter, either

When we add or subtract low-order terms, they disappear when using asymptotic notation. For example, consider the function n2 + 1000n. I claim that this function is Θ(n2). Clearly, if I choose c1 = 1, then I have n2 + 1000n ≥ c1n2, so this side of the inequality is taken care of.

The other side is a bit tougher. I need to find a constant c2 such that for sufficiently large n, I'll get that n2 + 1000n ≤ c2n2. Subtracting n2 from both sides gives 1000n ≤ c2n2 – n2 = (c2 – 1) n2. Dividing both sides by (c2 – 1) n gives 1000 / (c2 – 1) ≤ n. Now I have some flexibility, which I'll use as follows. I pick c2 = 2, so that the inequality becomes 1000 / (2 – 1) ≤ n, or 1000 ≤ n. Now I'm in good shape, because I have shown that if I choose n0 = 1000 and c2 = 2, then for all n ≥ n0, I have 1000 ≤ n, which we saw is equivalent to n2 + 1000n ≤ c2n2.

The point of this example is to show that adding or subtracting low-order terms just changes the n0 that we use. In our practical use of asymptotic notation, we can just drop low-order terms.

Combining them

In combination, constant factors and low-order terms don't matter. If we see a function like 1000n2 – 200n, we can ignore the low-order term 200n and the constant factor 1000, and therefore we can say that 1000n2 – 200n is Θ(n2).

When to use O-notation vs. Θ-notation

As we have seen, we use O-notation for asymptotic upper bounds and Θ-notation for asymptotically tight bounds. Θ-notation is more precise than O-notation. Therefore, we prefer to use Θ-notation whenever it's appropriate to do so.

We shall see times, however, in which we cannot say that a running time is tight to within a constant factor both above and below. Sometimes, we can only bound a running time from above. In other words, we might only be able to say that the running time is no worse than a certain function of n, but it might be better. In such cases, we'll have to use O-notation, which is perfect for such situations.