Sep 23: Finish Image Processing. Arrays. Interfaces and Polymorphism


Code discussed in lecture

The part of these notes on arrays is a modified version of notes from CS 5. I will go over the highlights in class, but the details will be here for later study.

Arrays

You can think of an array like a table. You give an index and get or store an element. For example, here is a table of winners of the Preakness (the middle of the three races in horse racing's Triple Crown) in the 1950s, indexed by the year of the race:

Year (index) Winner (element)
1950 Hill Prince
1951 Bold
1952 Blue Man
1953 Native Dancer
1954 Hasty Road
1955 Nashua
1956 Fabius
1957 Bold Ruler
1958 Tim Tam
1959 Royal Orbit

There is one difference between this table and arrays in Java: in Java, array indices always start at 0. So array indices always go as 0, 1, 2, 3, 4, … . (Java is different from languages such as Pascal, where you can select a lower bound other than 0. In C/C++, indices always start at 0, just as in Java.)

Then again, just because indices start at 0, that doesn't mean you always have to use all the entries starting from 0. If you'd rather start from 1, go ahead. The cost is just the wasted space of the 0-indexed entry.

Although this example has character strings (the names of the winning ponies) as its entries, we can store any type in the array, as long as all entries are declared as the same type. So for starters, our array entries will be something simpler, such as integers.

To declare an array of 10 ints you have to do two steps:

  1. Create a variable that can hold a reference to an array of the proper type.
  2. Create the actual array by using new.
int [] bozo; bozo = new int[10]; This style is reminiscent of objects, and arrays are a special kind of object. As with objects, we can combine the two lines above into one: int [] bozo = new int[10]; Our picture is the following:

Here,

The 10 elements of this array are bozo[0], bozo[1], bozo[2], …, bozo[9]. Note that
An array of n elements has elements indexed from 0 to n–1, only. An array of n elements does not have an element with index n.
It will soon become natural to start counting from 0.

You can think of array indices as being like subscripts. Our array bozo is like having bozo0, bozo1, bozo2, …, bozo9.

Technically, since an array is an object, we should not say that bozo is an array; we should say that bozo is a reference to an array. That would become incredibly tedious, however, and so we shall sometimes just say that bozo is an array. But you should understand that arrays are always objects, and that when we declare a variable to be an array, it's really a reference to an array.

You can make arrays of other sizes and of other types. To make an array blap of 30 doubles:

double [] blap = new double[30];

Array elements can be of any type. Even objects. Even other arrays!

Our first example of an array is in ShortList.java. We have a 10-element array named list. The first for-loop assigns the value i+1 to list[i] for i = 0, 1, …, 9. For example, list[5] is assigned the value 6.

Note how we set up the first for-loop:

for (int i = 0; i < N; i++) This will be a very common paradigm for stepping through an N-element array. We start at 0 and continue as long as the index is strictly less than N. As soon as it hits N, we are out of bounds of the legal array indices, so we must stop. In other words, the loop test i <= N would be wrong, because within the loop body, we would be trying to access list[N], and no such array entry exists. An attempt to access list[N] (or any other array element out of range) would cause an ArrayIndexOutOfBoundsException error at run time. (This situation shows another advantage of Java over C/C++, which would happily make the reference, returning garbage or overwriting other data or code).

Remember:

The legal indices into an array of n elements are integers in the range 0, 1, …, n–1. There is no element with index n. No indices are allowed to be negative, and no indices are allowed to be greater than or equal to n.

The most common paradigm for processing each element of an n-element array has a for-loop with the header

for (int i = 0; i < n; i++) and the body uses the variable i to index into the array.

The second for-loop prints out the values in the array in increasing order of the index. That is, it prints in order list[0], list[1], list[2], up through list[9].

Java 5.0 added another way to access every element of an array. The third loop in ShortList.java shows it:

for (int element : list) { // Print it out in increasing order using a foreach loop System.out.print(element + " "); } This style of loop is called a foreach-loop or foreach statement. The idea is that the loop variable, which is element in this example, takes on each value in the array (list in this example). In each iteration of the foreach-loop, the loop variable takes on the next value in the array.

Foreach-loops have the advantage that you cannot make an indexing error. You don't have to worry about indices being too large or too small. There are a few disadvantages to foreach-loops, however:

The bottom line on foreach-loops is that for the restricted cases in which they apply, they are wonderful. For all other cases (such as those listed above), you are best off avoiding them and instead using for-loops with explicit index variables (such as the first for-loop in ShortList.java).

The fourth for-loop prints out the values in decreasing order of the index: list[9], list[8], list[7], down through list[0]. Note how the loop index i decreases in this loop. We could not have used a foreach-loop for this job.

The fifth for-loop prints out the array in decreasing order again, but using a slightly different method. The loop index i increases, but we use a more complex expression, N-i-1, in the array index. When i is 0, N-i-1 is 9. When i is 1, N-i-1 is 8, and so forth. Finally, when i is 9, N-i-1 is 0. This for-loop points out that the array index in a program can be any expression that evaluates to an integer in the correct range of indices.

There is an alternate way to create an array, using an initializer list.

int [] list2 = {1, 3, 5, 9};

Instead of calling new, we put a list of numbers in curly braces on the right side of the assignment statement. The Java compiler counts the number of items in the list, verifies that they are all of type int, and creates an array of that length with the first item assigned to list2[0], the second to list2[1], etc. Only valid when you declare the array!

Note that when you do this that you don't necessarily know the length of the array. But the program shows how to deal with this: list2.length gives the length of the array list2.

Multidimensional arrays

In a multidimensional array, you can think of the array entries as themselves being arrays. For example, suppose we have the declaration

Rect [][] box = new Rect[6][8]; where Rect is a class. The usual way to think of box is as a 2-dimensional array with 6 rows and 8 columns:

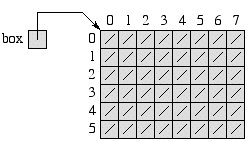
Note that the entry in row i and column j is denoted box[i][j]. In some other languages, you might write box[i,j], but not in Java (also not in C/C++). You must always use a separate set of brackets for each index: box[i][j].

A more accurate picture notes that we really have an array of 6 entries, each of which is an array of 8 entries. Therefore box[i] is a 1D array of references to Rect. The picture is:

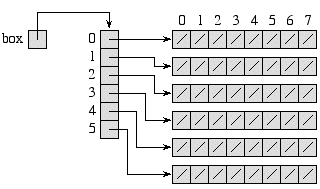
A consequence of the fact that 2D arrays are really arrays of arrays is that the number of rows is bozo.length and the number of columns is bozo[0].length. (Any valid subscript could be substituted for 0.)

Note that so far all of the references in box are null. After we assign a Rect object to each reference the picture would look like:

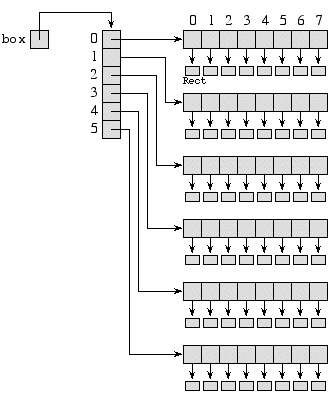
You can also use initializers with 2D arrays. The short assignment wants you to use a 3x3 matrix of weights. It suggests that one matrix that you should test is: 

float [][] edges = {{-1.0f, -1.0f, -1.0f},
                    {-1.0f, 8.0f, -1.0f},
                    {-1.0f, -1.0f, -1.0f}};

This is an array with three arrays of floats (one per row), each of which contains three floats.

Code for Image Manipulation

Let's look at some code now.

pickAndShow does what you did by hand in SA-0. It is static, so called on class name. Uses a Picture constructor that takes a file name. copy creates a copy by using a constructor that takes a Picture and returns a new copy of it.

What about increaseRed? It uses getPixels defined in SimplePicture. What comes back is an array of Pixel.

increaseRed uses a special foreach form of the for statement to go throught all of the pixels one at a time. As we suspected, it sets the red on each pixel to twice its current value. Note the use of method calls on the pixel to get and set the amount of red in the pixel. Note that we can use methods from the Pixel class without ever looking at the code.

The two decreaseRed methods are very similar to increaseRed. They get the amount of red, reduce it (by half for the first version, but a given amount for the second), and setRed to the new value. Howver, the first uses a while loop and the second a conventional for loop to go through the array. Barb Ericson is getting pedagogical and demonstrating various options.

Negate is also similar to increaseRed, but it creates a new Color object. Color is a Java library type used to represent and manipulate colors. As we suspected, it gets each color from the pixel. If a color value is c this method sets it to (255 - c).

flip does what we thought it did. But instead of getting an array of pixels it needs to access each one individually. It uses getPixel to do this. It first creates an new "empty" image of the correct size, which it calls target. It gets a pixel from the source, the corresponding one from the target, and sets the target's color to the source's color.

The outer for loop here has two initializations and two updates, one value increasing while the other is decreasing for the x values. The two y values in the inner for loop are kind of overkill. srcY and trgY are always equal! Could have used a single y variable for both.

Look at compose. Code similar to flip, in that for every pixel in the source it gets the corresponding target pixel in the target and sets the color of the target to the color of the source. But the way that it finds corresponding pixels is different. Note that it does an if test to make sure that we are still in the picture before updating the pixel, so don't go out of bounds. blueScreen has a very similar structure, but it puts the test for going out of bounds in the for loop tests rather than an if (more efficient). Also, it only copies if the amount of blue is less that the total amount of red and green.

scale is interesting. Demo. How do you scale a picture? Create an empty picture of the right size, and for each pixel in the new picture find the "corresponding" pixel in the old and copy it. Go through target in size 1 steps, original in size 1/factor steps. Note +=.

Polymorphism and Interfaces

Polymorphism comes from Greek words for "many" and "shape". So a polymorphic variable is one that can hold multiple types. It is easy to see why Simula found this idea helpful. In simulation you may have many objects, perhaps representing animals. It would be useful to have an array that could hold any animal type. The first object in the array might be a fish, the second a frog, the third an antelope, etc. For the simulation it would be useful to be able to go through the array and tell each animal to move. The fish would swim, the frog would hop, the antelope would run, etc. So we want to be able to have an array of type Animal. Fish, Frog, Antelope, etc. would be subtypes of Animal. They should be able to do anything that a generic Animal can do, perhaps plus other things as well.

Java gives us two ways to achieve this type of polymorphism. The first is to create an interface. That is what we will consider for the rest of this lecture. The second is inheritance, which we will see next class.

An interface is like a class where the method headers (name, return type, parameters) are given, but there are no bodies that implement these methods. We will see a large number of interfaces this term, because interfaces are ideal for specifying an Abstract Data Types (ADTs). An ADT consists of some data and a collection of operations that can be performed on that data. "A collection of operations" is exactly what an interface defines. We will see interfaces List, Set, Map, and many others.

Let's look at a simple interface and how it can be used. The file GeomShape.java contains such an interface. It looks at first like a class definition, but instead of using the word class in the header, it uses the word interface. The other difference is that the methods are not implemented. Instead of a method body, each one has a semicolon after the method header. This makes them abstract methods. An interface can have only abstract methods and constants.

The classes Circle.java and Rectangle.java both implement the GeomShape interface. Note that the the first line of the definition of both classes ends with implements GeomShape. (There could be a list of interface names, separated by commas.) The implements tag is a promise to include a definition for every abstract method in the interface. We say that the implementing class implements every method in the interface. It is an error to fail to implement any method from the interface, and the compiler will complain. (This is a slight lie - we will see later that classes can be abstract. But it is true about any class that can create objects.)

An implements tag is a promise to implement all the methods of the interface, but the class may include even more. For example, both the Circle and Rectangle class contain constructors and toString. Moreover, the Rectangle class has a flip method; the Circle class does not, but that's just to show you that the two classes need not implement the same exact set of methods, as long as each implements at least the methods in the interface (which are the methods it has promised to implement).

The advantage is that a variable (including a formal parameter) can be declared using the interface name as if it were a class name. As long as the object actually referenced by the variable is from a class that implements the interface, it's OK. For example, we can declare a variable to be a reference to a GeomShape and have it actually be a reference to a Circle, a reference to a Rectangle, or for that matter a reference to any class that implements GeomShape. We can call any of the methods specified in the interface on the object. We know that the methods specified in the interface are defined for the object, because that's exactly what the implements tag tells us.

The program GeomShapeDriver.java demonstrates our interface in action. The main method creates an array shapes that contains references to GeomShape objects. shapes[0] refers to a Circle and shapes[1] refers to a Rectangle. In the for loop the methods areaOf, move, and scale are called on shapes[0] the first time through the loop and on shapes[1] the second time through the loop. Java uses the actual type of the object referenced by shapes[i] to decide at run time which areaOf, move, and scale methods to call. Deciding at run time which method is actually called is known as dynamic binding. It is a feature of polymorphism: the ability of a single variable to reference more than one type of object. It can be quite powerful.

Let's revisit what is happening here, because it is important and also very cool. We have declared shapes as an array of type reference to GeomShape. Except that there's no such thing as a GeomShape object. GeomShape is a placeholder for any class that implements the scale, move, and areaOf methods that appear in the GeomShape interface declaration. When we actually create an object that implements GeomShape, say a Circle, we may assign the reference to that object to a place in shapes.

The truly remarkable part happens when we call a method with shapes[i] as the reference to the left of the dot, e.g., shapes[i].areaOf(). At compile time, we have no idea from which class the object will actually be. Perhaps shapes[i] references a Circle, but perhaps shapes[i] references a Rectangle. We don't know at compile time. And it doesn't matter! The decision as to which areaOf method gets called—the one in Circle or the one in Rectangle—is based entirely on what kind of object shapes[i] references at the time the call is made. That's dynamic binding.

An addtional observation: there is an if-statement that tests if shapes[i] is of type Rectangle. That is what the operator instanceof tests. There is a call to flip inside this if-statement. To make this call, we have to cast the variable shapes[i] to be a reference to a Rectangle object, because GeomShape does not include a flip method. Therefore, there is no reason for the compiler to treat as legal a call of flip on an object that implements GeomShape. We know that shapes[i] references a Rectangle at that moment, and so we are willing to assume responsibility for the call to shape being legal. In order to convince the compiler that the call is legal, however, we cast shapes[i] to a reference to Rectangle. The compiler then follows President Reagan's maxim: "Trust but verify." Because it is doing something that may be unsafe, it puts in a runtime test to make sure that shapes[i] really refers to a Rectangle before it allows the call to flip.

What would have happened if we had tried to cast shapes[i] to a reference to Rectangle when it actually was a reference to some other kind of object (such as a Circle)? We would get a run-time error known as a ClassCastException, and our program would crash at that point. You can see this behavior yourself: eliminate the if-statement that tests if shapes[i] is an instance of Rectangle.