Oct 18: Heaps and Priority Queues
Code discussed in lecture
- MinPriorityQueue.java
- ArrayListMinPriorityQueue.java
- SortedArrayListMinPriorityQueue.java
- HeapMinPriorityQueue.java
- Heapsort.java
Priority Queues
A priority queue is a queue which instead of being FIFO is Best Out. "Best" is defined by a priority. For a typical priority queue, low priority numbers are removed first. That may seem backwards, but think of "you are our number one priority!" That's better than being their number two or three priority.
There are hundreds of applications of priority queues. They come up in computer systems (high-priority print jobs, various priority levels of jobs running on a time sharing system, ...). They are used in finding shortest paths and other search problems. And a priority queue gives you an easy way to sort - put everything into the priority queue, then take them out one at a time. They come out in sorted order.
Min-priority queues also form the heart of discrete event simulators.
A discrete event simulator simulates a system in
which events occur. Each event occurs at some moment in time. The
simulation runs through time, where the time of each occurrence is
nondecreasing (i.e., the simulated time either increases or stays the
same—it never backs up). An event can cause another event to
occur at some later time. A min-priority queue keeps track of the
events that have yet to occur, with the key of an element being the
time that its event is to occur. When an event is created, the
insert method adds it to the min-priority queue. The
extractMin method tells us the next event to occur,
removing it from the queue so that we don't try to process it more
than once. Sometimes, the result of an event is to allow some other
event, already scheduled, to occur even earlier; in this case, the
decreaseKey method changes the time that the other event
occurs to move it earlier.
MinPriorityQueue.java
contains the interface for a min-priority queue.
Here, each element has a value, which we call its
key. The MinPriorityQueue interface
supports the following operations:
-
isEmpty, a predicate that tells whether the priority queue is empty. -
insert, which inserts an element into the priority queue. -
minimum, which returns the element in the priority queue with the smallest key, but leaves the element in the priority queue. -
extractMin, which returns the element in the priority queue with the smallest key and removes it from the priority queue.
decreaseKey
operation, which reduces the priority value in a given node, but this complicates
the job of implementing a priority queue. You will see how to handle this if
you take CS 31.)
We can also define a max-priority queue, which
replaces the latter operations by maximum and
extractMax (and increaseKey if you include it).
We will focus on min-priority queues, but they are really the same thing.
Java provides a class java.util.PriorityQueue, although
surprisingly no interface for a general prioritiy queue. This implementation
is based on a heap, which we will see later in this class. However, as
usual Java chooses different names. The correspondence is:
insertbecomesaddminimumbecomespeekextractMinbecomesremoveisEmptyremainsisEmpty
The way that we have defined the MinPriorityQueue
interface, the generic type is <E extends Comparable<E>>.
This says that you can use any type E that extends the Comparable
interface. But wait, you implement an interface, not extend it. In the context of
generic types, you always extend, even if you do it by implementing. Foolish
consistency is the hobgoblin of little minds.
What is the Comparable interface? It is the standard Java interface for
comparing two objects for less than, greater than, or equal. You need to implement a
single method, compareTo(other). It is used to compare this object to the other object.
The result is an integer which is negative for less than, 0 for equal, and positive for
greater than. A typical use taken from a program that we will see later today is:
if (list.get(smallest).compareTo(list.get(i)) > 0)Note that this asks if list.get(smallest) > list.get(i). To test less
than you would say < 0 and to test equality you would say == 0.
There is another way to compare two objects: the Comparator interface.
The book discusses this on p. 341. You implement the method compare(a, b)
and give the same negative, zero, or positive result as in compareTo. The
Java PriorityQueue class will use "natural order" (meaning the results of
compareTo) if you call the constructor with no arguments. If you want to use a Comparator
you call a constructor that takes two arguments: the initial size of the queue and a
Comparator object. This is more flexible, because you can define different orders
for different purposes.
Priority Queue Implementations
We will look at three implementations of priority queues. Each has different run times for the various operations. This leads to tradeoffs on which you want to use.
A min-priority queue implemented by an unsorted arraylist
The simplest way to implement a min-priority queue is by an arraylist whose elements may appear in any order. ArrayListMinPriorityQueue.java gives such an implementation.
The methods of this class, which implements the
MinPriorityQueue interface, are straightforward.
The private method indexOfMinimum computes and returns
the index in the array of the element with the smallest key. This
method is called by the minimum and
extractMin methods. extractMin seems a
bit strange. Instead of removing the smallest element it moves
the last element to the place where the smallest element was and
then removes the last element. It does this because removing the
last element is faster than removing an element from the middle of
the arraylist.
Let's look at the worst-case running times of the min-priority queue operations in this implementation. We express them in terms of the number n of elements that will ever be in the min-priority queue at any one time.
-
isEmptyjust returns a boolean indicating whether the size of the arraylist is zero. This method takes constant time, or Θ(1). -
insertjust adds a new reference at the end of the arraylist, and so it takes Θ(1) amortized time. - Both the
minimumandextractMinmethods callindexOfMinimumto find the element with the smallest key. This helper method takes Θ(n) time to search through n elements, and therefore so dominimumandextractMin.
A min-priority queue implemented by a sorted arraylist
The biggest disadvantage of implementing a min-priority queue by an unsorted arraylist is thatminimum and
extractMin take Θ(n) time. We can get the
running time of these operations down to Θ(1) if we keep the
arraylist sorted between operations. SortedArrayListMinPriorityQueue.java
gives this implementation. An important
detail is that it is sorted in decreasing order, so that the last position
is the minimum.
The minimum method is simpler now: it just returns the
element in position size-1 of the arraylist. The
extractMin method removes and returns
the element in position size-1. Thus both of these operations
take Θ(1) time.
The tradeoff is that, although minimum and extractMin
now take only
Θ(1) time, we find that insert takes
O(n) time. So we have not improved matters by
maintaining the array as sorted, unless we are making a lot more calls
to minimum and extractMin than to insert.
In practice,
the number of calls to extractMin is often the same as the number of
calls to insert, so we gain no overall advantage from keeping the
array sorted.
So can we do better? Yes, we can use a data structure called a heap.
Heaps
Heaps are based on binary trees. We have seen a few binary trees already in this course. We call the unique node above a node, say node i, the parent of i. The nodes below node i are the children of i. In a binary tree, every node has 0, 1, or 2 children. The line we draw between two nodes represents an edge.A heap is an array that we can view as a "nearly complete" binary tree. In other words, we fill in the tree from the root down toward the leaves, level by level, not starting a new level until we have filled the previous level. This is the shape property of a heap. For example, here's a heap and its representation in an array (the same representation works for an arraylist). Each node of the heap has its index in the array appearing above the node, and its contents appear within the node.
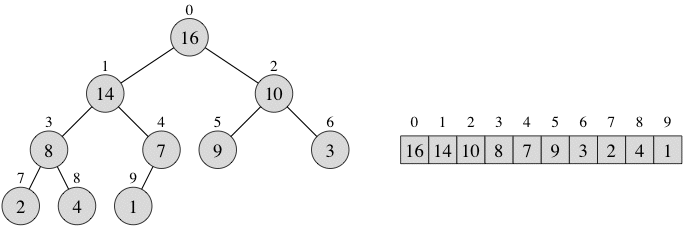
It's easy to compute the array index of a node's parent, left child, or right child, given the array index i of the node:
- The parent is at index (i-1)/2 (using integer division).
- The left child is at index 2*i + 1.
- The right child is at index 2*i + 2.
There are actually two kinds of heaps: max-heaps and min-heaps. In both kinds, the values in the nodes satisfy a heap property, the specifics depending on whether we're talking about a max-heap or a min-heap.
In a max-heap, the nodes satisfy the max-heap property:
For every node i other than the root, the value in the parent of node i is greater than or equal to the value in node i.In other words, the value in a node is at most the value in its parent. The largest value in a max-heap must be at the root. A subtree consists of a node and all the nodes below it, either directly or indirectly, and therefore the largest value in a subtree must be at the root of the subtree. The heap in the figure above is a max-heap.
A min-heap is defined in the opposite way, so that the min-heap property is
For every node i other than the root, the value in the parent of node i is less than or equal to the value in node i.In other words, the value in a node is at least the value in its parent. The smallest value in a min-heap must be at the root.
We define the height of a heap to be the number of edges on the longest path from the root down to a leaf. (Recall that a leaf is a node with no children.) The height of a heap with n nodes is Θ(lg n). (More precisely, the height is the greatest integer less than or equal to lg n.) Showing this property is not too hard, and the book does so on p. 352.
Operations on a heap
We want to allow two operations on a max-heap: insert a new item, and delete the maximum item. In both operations we want to maintain both the shape and heap properties. The trick is for both operations is to fix the shape first, and then to fix the heap property.Let's consider insert. Suppose we want to insert 15 in the heap shown above. By the shape property, it should go into the position to the right of the value 1, which would be position 10 in the array. (Representing the heap in an ArrayList makes this insertion particularly easy.) So if we put 15 into position 10 the shape property is statisfied.
But what about the heap property? Everything is fine, with the possible exception that the newly inserted item might be bigger than its parent. (It is in our example.) But that is easy to fix - swap the parent and the newly inserted child. But the new parent may be bigger than its parent (originally its grandparent). We repeatedly swap until the newly inserted item is less than or equal to its parent or reaches the root. (In our example this would be when it arrives in node 1, where 14 was originally.)
What about deleting the maximum? Well, we know where the maximum is - it is at the root, position 0 of the array. But simply removing it would leave a hole, which is not allowed. Also, the heap has one fewer item, so the rightmost leaf at the bottom level has to disappear. We can fix both of these shape problems by moving the rightmost leaf (last item in the occupied portion of the array) to the root (position 0) and decrementing the size of the occupied portion of the array.
What does this do to the heap property? The left and right subtrees of the root are both valid heaps. But the root might be smaller than one or both of its children. Again, this is easy to fix - swap the root with its larger child. Its larger child will be bigger the original root, everything in its subtree, and the smaller child (and thus everything in the smaller child's subtree). Thus it is the largest thing in the array and should be the new root. But this moves the problem down into the subtree - the value swapped into the subtree's root may violate the heap property of the subtree. But this is the same problem - we can repeat the operation until the thing moved to the root is a leaf or larger than its child or children. (Recursion can be used for both this and for insertion.)
An implementation of a min-heap in an arraylist is in HeapMinPriorityQueue.java. It shows how to implement the operations described above.
Let's look at the worst-case running times of the min-priority queue operations in this implementation. We express them in terms of the number n of elements that will ever be in the min-priority queue at any one time.
-
isEmptyjust returns a boolean indicating whether the size of the arraylist is zero. This method takes constant time, or Θ(1). -
insertfirst adds a new reference at the end of the arraylist, which takes Θ(1) amortized time. It then has to bubble the value up the heap until it is less than its parent. This takes at most the height of the heap swaps, which takes O(lg n) time. - The
minimummethod just has to return what is in position 0 of the arraylist. This takes Θ(1) time. - The
extractMinmethod returns the element in position 0 and puts the last element in its place. This takes Θ(1) time. However, it then has to restore the heap property, so it has to trickle the new root down until it is smaller than both children or is a leaf. This also takes at most the height of the heap swaps, which takes O(lg n) time.
Heapsort
A heap is the basis of a sorting algorithm called heapsort. Its running time is O(n lg n), and it sorts in place. That is, it needs no additional space for copying things (as mergesort does) or for a stack of recursive calls (quicksort and mergesort). It is a version of Selection Sort, but instead of running through the entire remaining array to find the next smallest item it uses a heap to organize information.Implementing heapsort
Heapsort has two major phases. First, given an array of values in an unknown order, we have to rearrange the values to obey the max-heap property. That is, we have to build a heap. Then, once we've built the heap, we repeatedly pick out the maximum value in the heap—which we know is at the root—put it in an appropriate slot in the array (by swapping it with the value in that slot), and restore the max-heap property. Note how convenient this is - the next spot to be filled in in selection sort (chosing maximums rather than minimums) goes precisely at the place where the heap has to shrink to maintain the shape property!
The code for heapsort is in Heapsort.java.
At the bottom, you can
see some private methods that help out other methods in the class:
swap, leftChild, and
rightChild.
How to build a heap
The obvious way to build a heap is to start with an unordered array. The first item is a valid heap. We can then insert the second item into the heap, then the third, etc. After we have inserted the last item we have a valid heap. This works fine and leads to an O(n lg n) heapsort. However, we can avoid implementing the insert code and speed up the algorithm a bit by using the code to restore the heap property after a deletion instead. The idea seems a bit strange at first, but it is really quite clever.
The code to restore a heap after a deletion is in maxHeapify
method. It takes three parameters: the array a holding
the heap and indices i and lastLeaf into the
array. The heap is in the subarray a[i..lastLeaf], and
when maxHeapify is called, we assume that the max-heap
property holds everywhere except possibly among node i
and its children. maxHeapify restores the max-heap
property everywhere.
maxHeapify works as follows. It computes the indices
left and right of the left and right
children of node i, if it has such children. Node
i has a left child if the index left is no
greater than the index lastLeaf of the last leaf in the
entire heap, and similarly for the right child.
maxHeapify then determines which node, out of node
i and its children, has the largest value, storing the
index of this node in the variable largest. First, if
there's a left child, then whichever of node i and its
left child has the larger value is stored in largest.
Then, if there's a right child, whichever of the winner of the
previous comparison and the right child has the larger value is stored
in largest.
Once largest indexes the node with the largest value
among node i and its children, we check to see whether we
need to do anything. If largest equals i,
then the max-heap property already is satisfied, and we're done. Otherwise,
we swap the values in node i and node
largest. By swapping, however, we have put a new,
smaller value into node largest, which means that the
max-heap property might be violated among node largest
and its children. We call maxHeapify recursively, with
largest taking on the role of i, to correct
this possible violation.
Notice that in each recursive call of maxHeapify, the
value taken on by i is one level further down in the
heap. The total number of recursive calls we can make, therefore, is
at most the height of the heap, which is Θ(lg n).
Because we might not go all the way down to a leaf (remember that we
stop once we find a node that does not violate the max-heap property),
the total number of recursive calls of maxHeapify is
O(lg n). Each call of maxHeapify takes
constant time, not counting the time for the recursive calls. The
total time for a call of maxHeapify, therefore, is
O(lg n).
Now that we know how to correct a single violation of the max-heap
property, we can build the entire heap from the bottom up. Suppose we
were to call maxHeapify on each leaf. Nothing would
change, because the only way that maxHeapify changes
anything is when there's a violation of the max-heap property among a
node and its children. Now suppose we called maxHeapify
on each node that has at least one child that's a leaf. Then
afterward, the max-heap property would hold at each of these nodes.
But it might not hold at the parents of these nodes. So we can call
maxHeapify on the parents of the nodes that we just fixed
up, and then on the parents of these nodes, and so on, up to
the root.
That's exactly how the buildMaxHeap method in Heapsort.java works. It computes the index
lastNonLeaf of the highest-indexed non-leaf node, and
then runs maxHeapify on nodes by decreasing index, all
the way up to the root.
You can see how buildMaxHeap works on our example heap,
including all the changes made by maxHeapify, by running
the slide show in this PowerPoint
presentation. Run it for 17 transitions, until you see the
message "Heap is built."
Let's analyze how long it takes to build a heap. We run
maxHeapify on at most half of the nodes, or at most
n/2 nodes. We have already established that each call of
maxHeapify takes O(lg n) time. The total
time to build a heap, therefore, is O(n lg n).
Because we are shooting for a sorting algorithm that takes
O(n lg n) time, we can be content with the
analysis that says it takes O(n lg n) time to
build a heap. It turns out, however, that a more rigorous analysis
shows that the total time to run the buildMaxHeap method
is only O(n).
Notice that most of the calls of maxHeapify made by
buildMaxHeap are on nodes close to a leaf. In fact,
about half of the nodes are leaves and take no time, a quarter of
the nodes are parents of leaves and require at most 1 swap, an eighth
of the nodes are parents of the parents of
leaves and take at most 2 swaps, and so on. If we sum the total number
of swaps it ends up being O(n).
Sorting once the heap has been built
The second phase of sorting is given by theheapsort
method in Heapsort.java. After it calls
buildMaxHeap so that the array obeys the max-heap
property, this method sorts the array. You can see how it works on
the example by running the rest of the slide show in this PowerPoint presentation.
Let's think about the array once the heap has been built. We know
that the largest value is in the root, node 0. And we know that the
largest value should go into the position currently occupied by the
last leaf in the heap. So we swap these two values, and declare that
the last position—where we just put the largest value—is
no longer in the heap. That is, the heap occupies the first
n-1 slots of the array, not the first n. The local
variable lastLeaf indexes the last leaf, so we decrement
it. By swapping a different value into the root, we might have caused
a violation of the max-heap property at the root. Fortunately, we
haven't touched any other nodes, and so we can call
maxHeapify on the root to restore the max-heap property.
We now have a heap with n-1 nodes, and the nth slot of
the array—a[n-1]—contains the largest element
from the original array, and this slot is no longer in the heap. So
we can now do the same thing, but now with the last leaf in
a[n-2]. Afterward, the second-largest element is in
a[n-2], this slot is no longer in the heap, and we have
run maxHeapify on the root to restore the max-heap
property. We continue on in this way, until the only node that we
have not put into the heap is node 0, the root. By then, it must
contain the smallest value, and we can just declare that we're done.
(This idea is analogous to how we finished up selection sort, where we
put the n-1 smallest values into the first n-1 slots of
the array. We then declared that we were done, since the only
remaining value must be the smallest, and it's already in its correct
place.)
Analyzing this second phase is easy. The while-loop runs n-1
times (once for each node other than node 0). In each iteration,
swapping node values and decrementing lastLeaf take
constant time. Each call of maxHeapify takes O(lg
n) time, for a total of O(n lg n) time.
Adding in the O(n lg n) time to build the heap
gives a total sorting time of O(n lg n).