About Schedule Software

PS-2, due Oct 11

I suggest start on this problem set early. If you start early, you are likely not to find it difficult at all. On the other hand, if you start late and make some mistakes in manipulating references (which is easy to do when dealing with linked lists), you might panic and it may be too late to get help.

This assignment will give you experience with low-level data structure manipulations. Most of the time we will be using pre-packaged implementations of ADTs to solve problems. However, being able to write your own data structures to implement an ADT, when necessary, is a useful skill. It is also important to understand something about what is being hidden inside ADTs in order to be able to make intelligent tradeoffs.

Part 1: Modify SLL.java

We saw that a major drawback to SLL.java is the fact that deletion is an O(n) operation, because of the need to find the predecessor of the current item in order to delete it. In class I briefly mentioned a way to get around this problem by using a dummy list header and keeping track of the item before the current item. In this part of the assignment you will modify SLL.java to use this representation. I suggest renaming the class. Mine is called HeaderSLL, but you can choose whatever name that you like.

You could still call the instance variable current, but it is less confusing to call it currentPred or some such name. This is an excellent chance to use refactoring in Eclipse. Select the name "current" in its declaration, chose "Rename" from within the Refactor menu, change the name, and hit return. All instances of the variable get renamed. The comments don't need to change, because we still have the same idea of current. We have just changed how we represent it.

For the basic assignment you should eliminate the tail instance variable. Updating this efficiently turns out to be trickier than it would first appear. Keeping track of the tail of the list will be extra credit.

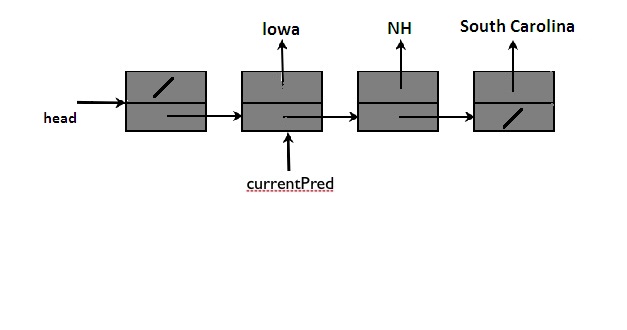
Our SLL with dummy header and currentPred is shown below. The first element in the linked list (with data field null) is not part of the list represented. It is like the sentinel in SentinelDLL. It is there to make operations easier. This represents a list with 3 elements, not 4.

Note that the current item is "NH", because currentPred refers to the element before it in the list. Note that using this representation, deleting the current item will be the same no matter which item is deleted. You simply change the next field in the element referenced by currentPred. This is the advantage of having a dummy list head.

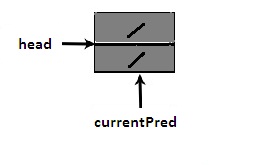
So what should an empty list look like? The following shows head, currentPred, and the dummy list header. Note that currentPred references the dummy list header rather than being null. But if you follow next from the dummy list header you get null, so this indicates that there is no current. This is the situation that will arise naturally if you remove the last item in the list, so it is more convenient than using currentPred == null as the test for no current.

Draw pictures of what the list should look like before and after various operations. Use them to figure out the names of fields that need to be changed and the values that they need to be changed to. In many cases the only change needed is to use currentPred.next in places that SLL.java used current.

Testing

Run your program with ListTest.java to demonstrate that it works. Notice that you have to change one line in ListTest.java in order to be able to test your implementation. Figure out which line it is and fix it.

Make sure to test all of the boundary cases - adding and removing at the front of the list, the end of the list, the middle of the list, etc. Make sure that things work correctly for an empty list. Your testing should not be random, but should be clearly organized and complete enough to convince us that your program works correctly.

Extra credit: Include tail

Create an instance variable tail and maintain it correctly as you do adds and removes. One thing that you will need to decide is whether tail should point to the last element in the list or to the element before the last element. (Note that head and currentPred point to the element before the one that they really mean.)

It is easy to introduce subtle bugs. Test your code carefully.

Please turn in a solution to the standard problem separately from the extra credit solution (i.e., keep the two solutions as different files). Solving the standard problem and then modifying it to use tail is probably easier than starting with the tail instance variable. Furthermore, by keeping them as two separate solutions, you will not be penalized in your regular grade for errors in the extra credit part.

Part 2: The Josephus problem

The general Josephus, whose band of 40 soldiers (plus himself) was once faced with certain defeat, proposed the following scheme for the remnants of his army to die honorably by their own hands. He arranged himself and his soldiers in a circle. Then, beginning with a particular soldier, they kept counting around in the circle and killing every other remaining soldier until only one remainded. Josephus proposed that this last soldier then commit suicide. But he cleverly arranged to be that last soldier himself and slipped away under cover of darkness.

You are to write a program to aid Josephus in figuring out where to stand in the circle. The program should read from the console window two numbers, the number of soldiers n and the number k skipped between successive executions. n should be at least 2, and k should be between 1 and n, inclusive. The program should then print out the execution order of the soldiers and the last soldier alive. Therefore the "classical" problem would have n = 41 (Josephus and 40 followers) and k = 2 (every second soldier dies). For n = 5 and k = 2, the order of death would be 2, 4, 1, 5, 3, and so Josephus should stand in position 3. For input pair n = 8 and k = 4, the order would be 4, 8, 5, 2, 1, 3, 7, 6. Note that the first soldier to die is always soldier number k. We call the output a permutation of the numbers 1, 2, …, n; that is, the output is some rearrangement of the first n integers.

Your program should create a circular doubly linked list using pointers to maintain the links. Do not use a sentinel in your circular list. (Even though we used a sentinel in the circular linked list in class, there is no rule that all circular lists must contain a sentinel. Also, there is no reason that your class needs to implement the interface we use for linked lists.) You can then run around the circle killing off soldiers by removing them from the circular list. Note that this has some similarity to the Duck, Duck, Goose program in the book, but uses a doubly linked list.

Testing

Generate runs for the following inputs:

n = 5, k = 2
n = 16, k = 3
n = 41, k = 2

Turn these in with your program listings.

Here is the output of my program for n = 5 and k = 2:

Enter number n of soldiers, at least 2: 5 Enter spacing between victims, between 1 and n: 2 Soldier 2 buys the farm. Soldier 4 buys the farm. Soldier 1 buys the farm. Soldier 5 buys the farm. The last remaining soldier is 3. And here is the beginning and end of my output for n = 41 and k = 2: Enter number n of soldiers, at least 2: 41 Enter spacing between victims, between 1 and n: 2 Soldier 2 buys the farm. Soldier 4 buys the farm. Soldier 6 buys the farm. Soldier 8 buys the farm. Soldier 10 buys the farm. ... Soldier 27 buys the farm. Soldier 3 buys the farm. Soldier 35 buys the farm. The last remaining soldier is 19.

Historical note

According to the Encyclopedia Brittanica, Flavius Josephus was a Jewish priest, scholar, and general. He was military commander of Galilee in 66 A.D. and held the fortress of Jotapata against the Romans for 47 days. After the city fell he took refuge with 40 followers in a nearby cave. The followers voted to commit suicide rather than surrender. Josephus disagreed with the decision but feared that he would be murdered if he made his views known. Therefore, he argued that because suicide was immoral, the men should stand in a circle and that each man in turn should kill the man next to the one next to him, around and around the circle, until only one man was left, and then only that man would have to kill himself. He then cleverly arranged to be the last man alive and surrendered to the Romans. (If you want historical accuracy, Josephus also convinced the second-to-last man to surrender rather than be killed, and Brittanica says only that the order was chosen "by lots.")

Extra credit: Cat world

In an alternate world, cats are the soldiers in the Josephus problem. But if you kill a cat once, it's not really dead. Cats have nine lives, you know, so you have to kill a cat nine times for it to be really dead.

It turns out that if all the cats have the same number of lives, the problem is not much more interesting than the "standard" Josephus problem, in which they have only one life. Instead, it's a little more interesting to vary the number of lives each cat has. Modify the Josephus problem so that the ith cat has i lives, for i = 1, 2, …, n. Only when a cat has no more lives should it be removed from the circle.

Here are two sample runs for my Cats program:

Enter number n of cats, at least 2: 5 Enter spacing between victims, between 1 and n: 2 Cat 1 turns in its Friskies. Cat 3 turns in its Friskies. Cat 2 turns in its Friskies. Cat 5 turns in its Friskies. The last remaining cat is 4.

Enter number n of cats, at least 2: 41 Enter spacing between victims, between 1 and n: 2 Cat 1 turns in its Friskies. Cat 3 turns in its Friskies. Cat 2 turns in its Friskies. Cat 5 turns in its Friskies. Cat 4 turns in its Friskies. ... Cat 39 turns in its Friskies. Cat 38 turns in its Friskies. Cat 41 turns in its Friskies. The last remaining cat is 40.

As usual, I encourage you to try other extra credit ideas. One possibility would be graphic and/or sound output for the Josephus problem.

Blackboard submission

Submit via Blackboard the zip file of a folder that contains the following files:

1. your modification of the SLL class.
2. test run for your modified SLL class.
3. classes you wrote for the Josephus problem.
4. test run requested for the Josephus problem: n = 5, k = 2; n = 16, k = 3; and n = 41, k = 2.
5. Additional files if you did the extra credit

Grading rubric

On programming assignments it is important to write the code well enough that it compiles and runs, enabling you to test it thoroughly and tune it to perfection. Therefore, starting with this problem set, there will be a much more severe deduction of points for code that does not compile and for code that compiles and runs but does not accomplish much.

Total of 125 points

Correctness, Efficiency, and Elegance of SLL Modifications (45 points)

10	Modify add
10	Modify remove
5	Modify getLast
5	Modify addFirst
5	Modify isEmpty, hasCurrent, and hasNext
10	Modify the other methods

Correctness, Efficiency, and Elegance of Josephus (40 points)

15	Create the circular doubly-linked list
10	Eliminate a single soldier correctly
10	Eliminate all soldiers except for the last one
5	Print appropriate commentary as the program progresses

Structure (15 points)

15	Good decomposition and organization.

Style (15 points)

2	Comments at top
5	Comments for methods (purpose, parameters, what is returned) in JavaDoc form.
5	Good names for methods, variables, parameters
3	Layout (blank lines, indentation, no line wraps, etc.)

Testing (10 points)

10	A run demonstrating the correctness of the modified SLL class and the three Josephus runs requested above.

Extra Credit

15	Adding tail reference and updating efficiently and correctly
10	Cats version of Josephus
?	Other ideas